Elliptic Curve Cryptography
1. Weierstrass 방정식
Weierstrass 방정식은 타원 곡선을 나타내는 기본적인 수식이다.

여기서:
- a1,a2,a3,a4,a6는 임의의 값(계수)이고,
- K는 이 방정식이 정의된 수 체계이다.(예: 실수나 유리수 등).
2. K의 특성(characteristic)이 2 또는 3이 아닌 경우

와 y를 다음과 같이 변환할 수 있다.
3. 변환 후 방정식

여기서 a,b∈K(a와 b는 K에 속하는 값)
4. 판별식(Discriminant)
이 곡선의 판별식(Discriminant)은 다음과 같이 계산:

판별식은 타원 곡선이 어떤 특성을 가지는지를 알려주는 중요한 값이다.
특히, Δ≠0 일 경우, 곡선은 비특이(non-singular) 상태를 갖는다.(즉, 매끄럽고 뾰족하지 않음).
Elliptic Curves Over R
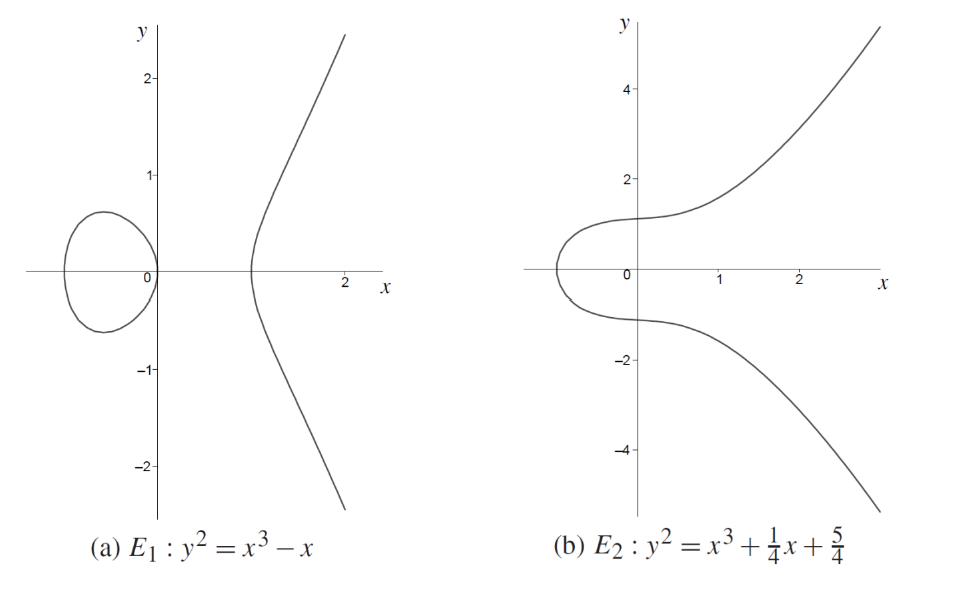
(a) 그래프를 보면
- 이 방정식은 a=−1, b=0인 경우에 해당
- 그래프에서 보이는 특징:
- x축에서 대칭 구조를 가진다.
- 아래쪽에는 닫힌 고리(루프)가 있고, 위쪽으로 뻗어나가는 두 개의 가지가 있다.
(b) 그래프
- 이 방정식은 a=1/4, b=5/4인 경우에 해당
- 그래프에서 보이는 특징:
- 곡선은 (x,y)(x, y) 평면에서 부드럽게 연결된 형태를 보임
- 루프처럼 보이지만, 위아래로 더 크게 퍼져 있는 구조.
* 타원 곡선의 중요한 특성
- 타원 곡선은 대칭적이다. 즉, y→−y 로 뒤집어도 동일한 곡선
- 이 그래프들은 "비특이(non-singular)" 상태를 나타내며, 이는 곡선이 매끄럽고 뾰족한 점이 없다는 것을 의미
Group Law(군연산)
군 연산이란?
- 타원 곡선 위의 점들을 더하거나(덧셈), 같은 점을 두 번 더하는(배가) 연산 규칙을 말함.
- 이 연산은 타원 곡선 암호학에서 중

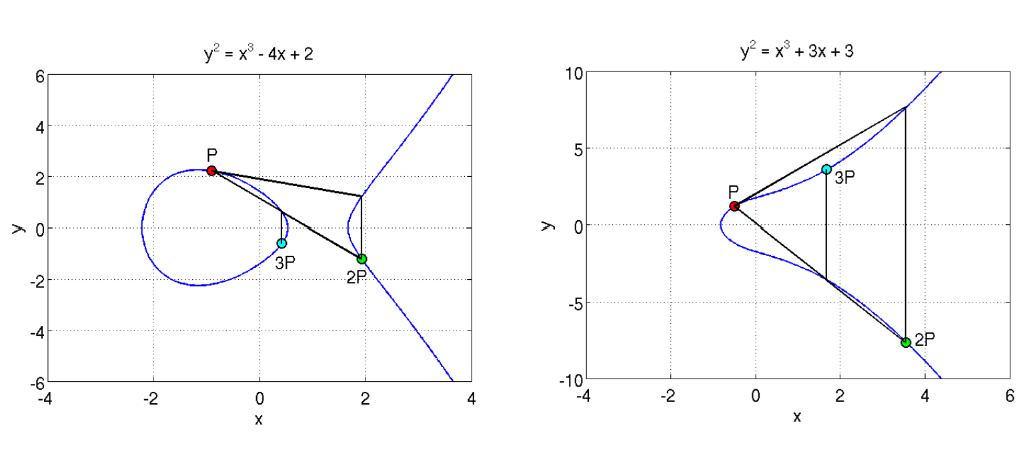
(a) Addition: P+Q=R
두 점 P(x1,y1)와 Q(x2,y2)를 더하는 방법.
과정:
- P와 Q를 잇는 직선을 그린다.
- 이 직선은 곡선을 한 번 더 교차한다. 교차점의 x-좌표를 , y-좌표를 y3라고 한다.
- 교차한 점의 대칭점(즉, y-값만 부호를 반대로 한 점)이 R(x3,y3)가 된다.
(b) Doubling: P+P=R
점 P(x1,y1)를 자기 자신과 더하는 방법.
과정:
- 점 P에서 곡선의 접선을 그림.
- 이 접선은 곡선을 한 번 더 교차. 교차점의 x-좌표를 , y-좌표를 y3 라고 함.
- 교차한 점의 대칭점이 가 된다.
1. 타원 곡선의 정의
타원 곡선은 방정식

정의되며, 여기서:
- a, b는 상수이고,
- char(K)≠2,3(수 체계 K의 특성이 2나 3이 아님).
2. 군 연산의 정의
타원 곡선에서의 연산 규칙은 다음과 같다:
1. 항등원 (Identity)
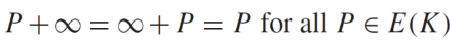
- 여기서 ∞는 "무한 원점"(Identity Point)이다.
- 곡선 상의 어떤 점 P에 를 더해도 결과는 P 그대로이다.
2. 반대 점 (Negatives)
- 곡선 위의 점 P=(x,y) ∈ E(K)에 대해, −P는 (x,−y)로 정의된다.
- 즉, −P는 P와 x-좌표는 같고 y-좌표만 부호가 반대인 점.
- P+(−P)가 성립한다.
- 또한 -∞= ∞
3. 점 덧셈 (Point Addition)
두 점 P=(x1,y1) ∈ E(K), Q=(x2,y2) ∈ E(K)에 대해 P≠±Q라면:
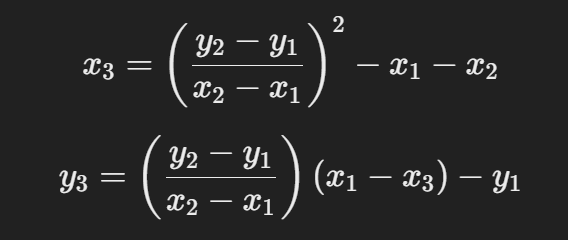

4. 점 배가 (Point Doubling)


유한체(Finite Field) 상에서 정의된 타원 곡선(Elliptic Curves over Finite Fields)

이 곡선은 유한체 위에서 정의되었다.
즉 소수 29를 (mod)으로 하는 산술로 이루어진다.
2. 판별식 Δ
Δ는 타원 곡선이 비특이(non-singular) 상태인지 확인하는 데 사용:

계산 결과:
Δ=−176896(mod 29) ≠ 0
따라서, 이 곡선은 F29 상에서 실제 타원 곡선임이 확인
E(F29)의 점은 다음과 같다

예문을 풀어보자
(1) (5,22) + (16,27)=???



(5,22)+(16,27)=(13,6) 이다.
(b) 2(5,22) =???



즉 2(5,22)= (14,6) 이다.

- 점의 대칭성: 곡선 위의 점들은 항상

- 에 대해 대칭입니다. 예를 들어, (0,1)와 (0,22).
- 점의 총 개수: 여기서 총 23개의 점이 있습니다(무한 원점 포함).
E23(1,1): y^2 = x^3+x+1 over F23
1. 점 P와 Q의 덧셈: P+
P=(3,10),
덧셈을 수행하기 위해 다음 과정을 거칩니다.
(a) 기울기 λ계산
기울기 λ는 두 점 P와 Q를 잇는 직선의 기울기로 정의된다.


(B) 분수 계산

따라서


(C) XR, YR 찾기

결과: P+Q=(17,20)
점 P의 배가: 2P
(a) 기울기 계산
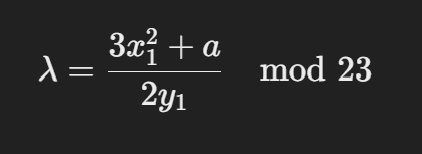

(b) 분수 계산(역원 구하기)
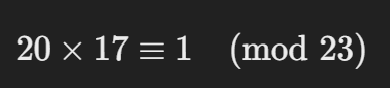


(c) XR, YR 구하기
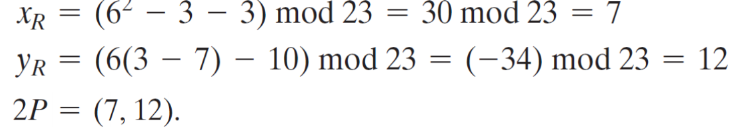
Elliptic Curve Point Addtion/ Doubling

Elliptic-Curve Diffie-Hellman(ECDH)
1. ECDH 개요
ECDH는 두 사용자가 타원 곡선을 기반으로 공통 비밀 키를 안전하게 생성할 수 있도록 도와주는 프로토콜
1단계: 곡선과 기준 점 P 선택
- Alice와 Bob은 미리 타원 곡선 E와 그 위의 기준 점 P를 선택.
- 이 곡선과 P는 모두에게 공개
2단계: Alice가 개인 키 a와 공개 키 pkA 생성
- Alice는 랜덤한 정수 a를 개인 키로 선택.
- 공개 키 pkA=를 계산하여 Bob에게 보낸다.
- 여기서 aP는 P를 a번 더한 점이다.
3단계: Bob이 개인 키 b와 공개 키 생성
- Bob도 랜덤한 정수 b를 개인 키로 선택한다.
- 공개 키 pkB를 계산하여 Alice에게 보내다.
4단계: Alice가 공유 비밀 키 계산
- Alice는 Bob이 보낸 공개 키 pkB=를 사용한다.
- a(pkB)=a(bP)=abP를 계산하여 공유 비밀 키를 생성.
5단계: Bob이 공유 비밀 키 계산
- Bob은 Alice가 보낸 공개 키 pkA=를 사용한다.
- b(pkA)=b(aP)=abP를 계산하여 동일한 공유 비밀 키를 생성
'SECURITY > CRYPTO' 카테고리의 다른 글
| [CRYPTO]Other_PublicKey_Cryptosystems (0) | 2024.12.04 |
|---|---|
| [CRYPTO] UserAuthentication (0) | 2024.12.04 |